5 Turtle-Grafiken

In der Computer-Graphik versteht man unter einer Turtle ein Zeichengerät, das sich schrittweise über eine Fläche bewegt und dabei mit einem Stift eine zusammenhängende Linie zeichnet. Die Turtle wird durch ein Computer-Programm gesteuert, das ihr einfache Kommandos geben kann. Zum Beispiel kann nach jedem Schritt die Richtung für den nächsten Schritt geändert werden. Heutzutage ist die Turtle kein mechanisches Gerät mehr, sondern wird auf dem Monitor simuliert.

Die klassische Computer-Sprache mit eingebauter Turtle-Graphik ist Logo (Netlogo, Logo Foundation). Schon einfache Logo-Programme können Graphiken mit komplexer Struktur und fraktalen Eigenschaften erzeugen (Logo Graphics Gallery->Recursive Graphic Designs).

Eine andere Möglichkeit, die Turtle zu steuern, sind Lindenmayer-Systeme (MathePrisma: Lindenmayersysteme, Fraktalwelt: L-Systems).

Die oben genannten Methoden zur Steuerung der Turtle sollen Bilder hoher Komplexität aus einfachen Regeln erzeugen, die rekursiv angewendet werden. Die Folge der Drehwinkel für die Turtle ist dabei mathematisch von einfacher Bauart. Verwendet man stattdessen eine mathematisch kompliziertere Folge wie z.B.

\[ \sqrt {2}\,n,\, n=1,2, \dots , \]

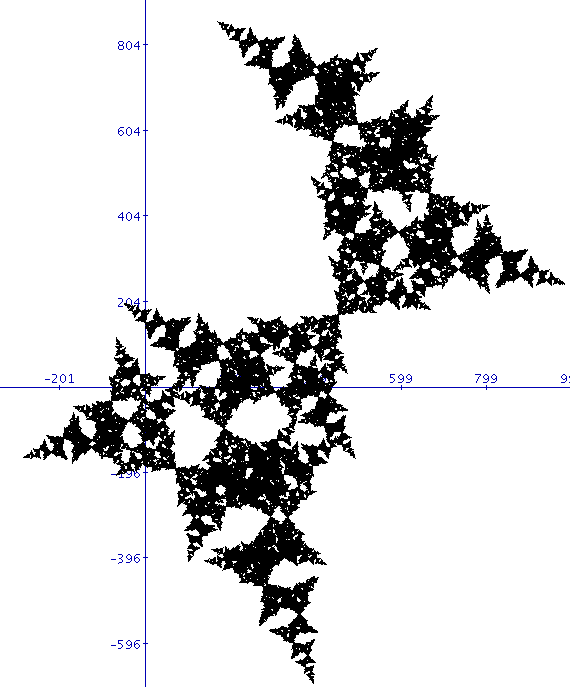
so erhält man eine Verbindung zur Theorie der Exponentialsummen. Die entstehenden Bilder zeigen unter Umständen geometrische Strukturen, deren Erklärung eine tiefere mathematische Analyse erfordert:

Turtle-Grafik zur Folge

Turtle-Galerie:

\( \sqrt {n},\, n=1,2, \ldots \) \( \log (n),\, n=1,2, \ldots \) \( \sin (\sqrt {n}),\, n=1,2, \ldots \) \( \sqrt {\log {n}}, n=1,2, \ldots \)
\( \sqrt {n}\sin {n},\, n=1,2, \ldots \) \( \sqrt {n}\log {n},\, n=1,2, \ldots \) \( \tan (\sqrt {n}),\, n=1,2, \ldots \) \( \sin (n^2),\, n=1,2, \ldots \)
\( \sqrt {2}\,n,\, n=1,2, \ldots \) \( \sqrt {2}\, n^2,\, n=1,2, \ldots \) \( \tan (n),\, n=1,2, \ldots , 200000 \) \( \tan (n),\, n=1,2, \ldots , 500000 \)
\( \tan (n),\, n=1,2, \ldots , 1000000 \) \( \sin (n \,\mbox {xor}\, 2),\, n=1,2, \ldots \) \( \sin (n \,\mbox {xor}\, 3),\, n=1,2, \ldots \) \( \sin (n \,\mbox {xor}\, 5),\, n=1,2, \ldots \)